Tutorial: Machine Learning-Informed Meta-Analysis

Tutorial Requirements

1. Install R and then RStudio
   • Follow the instructions here: https://posit.co/download/rstudio-desktop/
2. Open RStudio.
   Now, run the setup script for this workshop.
   In the window labeled “Console”, paste this code and press [Enter]:

source("https://raw.githubusercontent.com/cjvanlissa/meta_workshop/refs/heads/master/check_function.R")

3. If you have your own data: after running the source() command above, you can use the function check_data().
   • Load your own data into R as usual, and check if you can use it for the workshop exercises by running:
   • check_data(your_data_object)

Meta-Analysis in R

The essence of Meta-Analysis is pooling your effect sizes to get an overall effect size estimate of the studies.

When pooling effect sizes in Meta-Analysis, there are two basic approaches: the Fixed-Effect-Model, or the Random-Effects-Model (Borenstein et al. 2009). The fixed effect model assumes that one true effect size exists in the population; the random effects model assumes that the true effect varies (and is normally distributed).

Both of these models require an effect size, and a dispersion (variance) estimate for each study.

For these meta-analyses, we’ll use the metafor package (Viechtbauer 2010). However, notice that we load a different package, metaforest. The reason is that it contains the example data for this tutorial, and it loads the metafor package in turn.

library(metaforest)

Using Your Own Data

If you want, you can conduct the examples below with your own data. Note that the interactive questions won’t work in this case (the correct answers are based on the curry data).

If you want to use your own data, you can use the function check_data() to help make sure that your data are suitable for the tutorial examples. Install the function by running:

source("https://raw.githubusercontent.com/cjvanlissa/meta_workshop/refs/heads/master/check_function.R")

Then, apply the function to your data object by running check_data(your_data_object). It will give helpful suggestions to make it easier to follow the tutorial with your own data:

#> ✔ Looks like you're all set to do the workshop!

df <- curry
check_data(df)

#> There is no column named 'yi' in your data. If you have an effect size column, it will be easier to do the tutorial if you rename it, using syntax like this:
#>   
#>   names(df)[which(names(df) == 'youreffectsize')] <- 'yi'
#>   
#>   If you do not yet have an effect size column, you may need to compute it first. Run ?metafor::escalc to see the help for this function.

Note that the message suggests that we rename the effect size column, which is called d in the curry dataset, to yi. Let’s do that:

names(df)[which(names(df) == 'd')] <- 'yi'

Using Different Demo Data

If you do not have your own data but are up for a challenge, you can use a different demo dataset to complete the tutorial. Two suggestions are:

metaforest::fukkink_lont
pema::bonapersona

Fixed Effect Model

The idea behind the fixed-effects-model

The fixed-effects-model assumes that all observed effect sizes stem from a single true population effect (Borenstein et al. 2009). To calculate the overall effect, we therefore average all effect sizes, but give studies with greater precision a higher weight. Precision relates to the fact that studies with a smaller Standard Error provide more accurate estimates of the true population effect.

For this weighing, we use the inverse of the variance $1/\hat\sigma^2_k$ of each study $k$. We then calculate a weighted average of all studies, our fixed effect size estimator $\hat\theta_F$:

$$\begin{equation} \hat\theta_F = \frac{\sum\limits_{k=1}^K \hat\theta_k/ \hat\sigma^2_k}{\sum\limits_{k=1}^K 1/\hat\sigma^2_k} \end{equation}$$

These examples assume you already have a dataset with the calucated effects and SE for each study. The curry data set, inside the metaforest package, will do. This dataset already contains the effect sizes and their variances, so we can directly use the rma function.

Fixed-effects Model with rma

The rma() function has many arguments, all of which you can accessed by typing ?rma in your console once the metafor package is loaded, or selecting the function and pressing F1.

Here is a table with the most important arguments for our code:

Argument	Function
yi	A vector with the effect sizes
vi	A vector with the sampling variances
method	A character string, indicating what type of meta-analysis to run. FE runs a fixed-effect model

Let’s conduct our first fixed-effects-model Meta-Analysis. We we will give the results of this analysis the simple name m.

m <- rma(yi = df$yi,     # The yi-column of the df, which contains Cohen's d
         vi = df$vi,    # The vi-column of the df, which contains the variances
         method = "FE") # Run a fixed-effect model
m

#> Fixed-Effects Model (k = 56)
#> 
#> I^2 (total heterogeneity / total variability):   64.95%
#> H^2 (total variability / sampling variability):  2.85
#> 
#> Test for Heterogeneity:
#> Q(df = 55) = 156.9109, p-val < .0001
#> 
#> Model Results:
#> 
#> estimate      se    zval    pval   ci.lb   ci.ub      
#>   0.2059  0.0219  9.4135  <.0001  0.1630  0.2487  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

We now see a summary of the results of our Meta-Analysis, including

• The total number of included studies (k)
• The overall effect, its confidence interval and p-value
• The Q-test of heterogeneity

Formative Assessment

How big is the overall effect?

True or false: A significant proportion of the variability in effect sizes is attributable to heterogeneity, rather than sampling error. TRUE FALSE

What can you say about the heterogeneity of the population effect? It is assumed to be zero It is significant, Q(55) = 156,91, p < .0001 It is large, I2 = 64.95% Can’t say anything based on this output

Random-Effects-Model

We can only use the fixed-effect-model when we can assume that all included studies tap into one true effect size. In practice this is hardly ever the case: interventions may vary in certain characteristics, the sample used in each study might be slightly different, or its methods. If we can assume that there are many small, random, uncorrelated variations in true effect sizes, then a more appropriate assumption in these cases might be that the true effect size follows a normal distribution.

The Idea behind the Random-Effects-Model

In the Random-Effects-Model, we want to account for our assumption that the population effect size is normally distributed (Schwarzer, Carpenter, and Rücker 2015).

The fixed-effect-model assumes that when the observed effect size $\hat\theta_k$ of an individual study $k$ deviates from the true effect size $\theta_F$, the only reason for this is that the estimate is burdened by (sampling) error $\epsilon_k$.

$$\hat\theta_k = \theta_F + \epsilon_k$$

While the random-effects-model assumes that, in addition, there is a second source of error $\zeta_k$.This second source of error is introduced by the fact that even the true effect size $\theta_k$ of our study $k$ is also only part of an over-arching distribution of true effect sizes with the mean $\mu$(Borenstein et al. 2009).

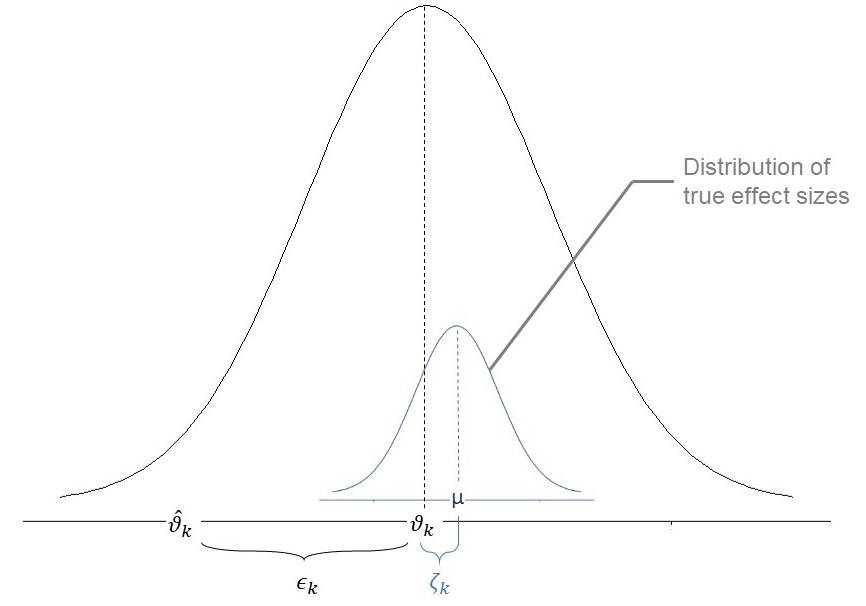
An illustration of parameters of the random-effects-model

The formula for the random-effects-model therefore looks like this:

$$\hat\theta_k = \mu + \epsilon_k + \zeta_k$$

When calculating a random-effects-model meta-analysis, where therefore also have to take the error $\zeta_k$ into account. To do this, we have to estimate the variance of the distribution of true effect sizes, which is denoted by $\tau^{2}$, or tau². There are several estimators for $\tau^{2}$, all of which are implemented in metafor.

Random-Effects Model with rma

We can re-use our code from the fixed-effects-model and simply remove the method = "FE" argument to conduct a random-effects analysis with the default REML estimator for $\tau^2$:

m_re <- rma(yi = df$yi,     # The yi-column of the df, which contains Cohen's d
            vi = df$vi)    # The vi-column of the df, which contains the variances
m_re

#> 
#> Random-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of total heterogeneity): 0.0570 (SE = 0.0176)
#> tau (square root of estimated tau^2 value):      0.2388
#> I^2 (total heterogeneity / total variability):   67.77%
#> H^2 (total variability / sampling variability):  3.10
#> 
#> Test for Heterogeneity:
#> Q(df = 55) = 156.9109, p-val < .0001
#> 
#> Model Results:
#> 
#> estimate      se    zval    pval   ci.lb   ci.ub      
#>   0.2393  0.0414  5.7805  <.0001  0.1581  0.3204  *** 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Formative Assessment

How big is the overall effect?

What is the estimated heterogeneity?

What can you say about the the expected value of the population effect in the random-effects model, compared to the previous fixed-effect model? It is larger It is smaller Can’t say anything based on this output It is about the same

This is caused by the fact that random-effects models assign more equal weight to all studies, including small ones, which tend to be more biased.

Meta-Regression

The idea behind meta-regression

In a conventional regression, we specify a model predicting the dependent variable $y$, across $_i$ participants, based on their values on $p$ predictor variables, $x_{i1} \dots x_{ip}$. The residual error is referred to as $\epsilon_i$. A standard regression equation therefore looks like this:

$$y_i=\beta_0 + \beta_1x_{1i} + ...+\beta_px_{pi} + \epsilon_i$$

In a meta-regression, we want to estimate the effect size $\theta$ of several studies $_k$, as a function of between-studies moderators. There are two sources of heterogeneity: sampling error, $\epsilon_k$, and between-studies heterogeneity, $\zeta_k$ so our regression looks like this:

$$\theta_k = \beta_0 + \beta_1x_{1k} + ... + \beta_px_{pk} + \epsilon_k + \zeta_k$$

You might have seen that when estimating the effect size $\theta_k$ of a study $k$ in our regression model, there are two extra terms in the equation, $\epsilon_k$ and $\zeta_k$. The same terms can also be found in the equation for the random-effects model. The two terms signify two types of independent errors which cause our regression prediction to be imperfect. The first one, $\epsilon_k$, is the sampling error through which the effect size of the study deviates from its “true” effect. The second one, $\zeta_k$, denotes that even the true effect size of the study is only sampled from an overarching distribution of effect sizes.

As the equation above has includes fixed effects (the $\beta$ coefficients) as well as random effects ($\zeta_k$), the model used in meta-regression is often called a mixed-effects-model.

Testing Moderators’ Significance

To evaluate the statistical significance of a predictor, we conduct a t-test (or Z-test) of its $\beta$-weight.

$$t=\frac{\beta}{SE_{\beta}}$$

Which provides a $p$-value telling us if a variable significantly predicts effect size differences in our regression model.

Assessing Meta-Regression Model Fit

In conventional regression, $R^2$ is commonly used to quantify the percentage of variance in the data explained by the model, as a percentage of total variance (0-100%). As this measure is commonly used, and many researchers know how to to interpret it, we can also calculate a $R^2$ analog for meta-regression using this formula:

$$R_2=\frac{\hat\tau^2_{REM}-\hat\tau^2_{MEM}}{\hat\tau^2_{REM}}$$

Where $\hat\tau^2_{REM}$ is the estimated total heterogenetiy based on the random-effects-model and $\hat\tau^2_{REM}$ the total heterogeneity of our mixed-effects regression model.

NOTE however, that $R^2$ refers to variance explained in the observed data. In linear regression, the more predictors you add, the better your model will explain the observed data. But this can decrease the generalizability of you model, through a process called overfitting: You’re capturing noise in your dataset, not true effects that exist in the real world. In meta-regression, because the estimate of heterogeneity may differ, we may not actually see the $R^2$ increasing with more predictors - but because the samples are often small, be very mindful of overfitting nonetheless.

Meta-regression in R

Meta-regressions can be conducted in R using the rma function in metafor. First, let’s conduct a regression with a single categorical predictor, donorcode, which has two levels: Anxious and Typical:

m_cat <- rma(yi ~ donorcode, vi = vi, data = df)
m_cat

#> 
#> Mixed-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.0567 (SE = 0.0177)
#> tau (square root of estimated tau^2 value):             0.2382
#> I^2 (residual heterogeneity / unaccounted variability): 67.81%
#> H^2 (unaccounted variability / sampling variability):   3.11
#> R^2 (amount of heterogeneity accounted for):            0.49%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 54) = 155.0054, p-val < .0001
#> 
#> Test of Moderators (coefficient 2):
#> QM(df = 1) = 1.5257, p-val = 0.2168
#> 
#> Model Results:
#> 
#>                   estimate      se    zval    pval    ci.lb   ci.ub    
#> intrcpt             0.0829  0.1332  0.6222  0.5338  -0.1781  0.3439    
#> donorcodeTypical    0.1730  0.1401  1.2352  0.2168  -0.1015  0.4476    
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

By default, metafor::rma() will recode factor variables to make one group the reference category and create dummies for all other groups. The syntax above created a binary indicator variable (a dummy variable) for people who fall in the Typical category. It then estimated the model intercept - which is the population effect size in the Anxious category, which serves as reference category here, and the effect of the donorcodeTypical dummy, which tells us the difference between the two groups’ population effects.

Formative Assessment

What is the expected population effect size in the Typical group?

What is the expected population effect size in the Anxious group?

True or false: There is a significant difference between the two groups. TRUE FALSE

Continuous Predictors

Imagine you want to check if the proportion of male participants is associated with effect size. The variable sex contains this information. You can use this predictor in a meta-regression:

m_reg <- rma(yi ~sex,
             vi = vi,
             data = df)
m_reg

#> 
#> Mixed-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.0544 (SE = 0.0173)
#> tau (square root of estimated tau^2 value):             0.2333
#> I^2 (residual heterogeneity / unaccounted variability): 66.50%
#> H^2 (unaccounted variability / sampling variability):   2.98
#> R^2 (amount of heterogeneity accounted for):            4.53%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 54) = 149.5878, p-val < .0001
#> 
#> Test of Moderators (coefficient 2):
#> QM(df = 1) = 2.1607, p-val = 0.1416
#> 
#> Model Results:
#> 
#>          estimate      se    zval    pval    ci.lb   ci.ub    
#> intrcpt    0.0648  0.1253  0.5168  0.6053  -0.1808  0.3104    
#> sex        0.0050  0.0034  1.4699  0.1416  -0.0017  0.0116    
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Formative Assessment

True or false: There is a significant effect of sex. TRUE FALSE

How to interpret the effect of sex? There is no effect of sex The difference between men and women is .005 1% increase in male participants is associated with .005 increase of the effect size Can’t say based on this output

Multiple Meta-Regression

Previously, we only considered the scenario in which we use one predictor $\beta_1x_1$ in our meta-regression. When we add more than one predictor, we’re using multiple meta-regression. In multiple meta-regression we use several moderators (variables) to predict the outcome (effect sizes). When we look back at the general meta-regression formula we defined before, we actually see that the formula already provides us with this feature through the $\beta_nx_{pk}$ part. Here, the parameter $p$ denotes that we can include $p$ more predictors/variables into our meta-regression, making it a multiple meta-regression.

We could include both predictors from the previous exercises in a mutliple meta-regression as follows:

m_multi <- rma(yi ~ sex + donorcode,
               vi = vi,
               data = df)
m_multi

#> 
#> Mixed-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.0551 (SE = 0.0175)
#> tau (square root of estimated tau^2 value):             0.2347
#> I^2 (residual heterogeneity / unaccounted variability): 66.89%
#> H^2 (unaccounted variability / sampling variability):   3.02
#> R^2 (amount of heterogeneity accounted for):            3.42%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 53) = 148.6166, p-val < .0001
#> 
#> Test of Moderators (coefficients 2:3):
#> QM(df = 2) = 3.0602, p-val = 0.2165
#> 
#> Model Results:
#> 
#>                   estimate      se     zval    pval    ci.lb   ci.ub    
#> intrcpt            -0.0337  0.1626  -0.2074  0.8357  -0.3523  0.2849    
#> sex                 0.0043  0.0035   1.2310  0.2183  -0.0025  0.0111    
#> donorcodeTypical    0.1361  0.1421   0.9579  0.3381  -0.1424  0.4146    
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Now, let’s create a model that includes all potential moderators of the effect size:

mods <- c("sex", "age", "location", "donorcode", "interventioncode", "controlcode", "recipients", "outcomecode")

res_multi2 <- rma(as.formula(paste("yi ~", paste(mods, collapse = "+"))), vi = vi, data = df)

res_multi2

#> 
#> Mixed-Effects Model (k = 56; tau^2 estimator: REML)
#> 
#> tau^2 (estimated amount of residual heterogeneity):     0.0038 (SE = 0.0076)
#> tau (square root of estimated tau^2 value):             0.0618
#> I^2 (residual heterogeneity / unaccounted variability): 12.55%
#> H^2 (unaccounted variability / sampling variability):   1.14
#> R^2 (amount of heterogeneity accounted for):            93.30%
#> 
#> Test for Residual Heterogeneity:
#> QE(df = 26) = 34.1905, p-val = 0.1303
#> 
#> Test of Moderators (coefficients 2:30):
#> QM(df = 29) = 105.3506, p-val < .0001
#> 
#> Model Results:
#> 
#> 
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Formative Assessment

What is the number of studies included in the second multiple meta-regression (with all predictors)?

What is the number of parameters of the second multiple meta-regression (with all predictors)?

The $R^2$ of the second multiple meta-regression model is 93.30%. How can we interpret this? With caution; the model is likely overfit. As a large effect; there must be several significant moderators. As a large effect; the moderators explain most of the heterogeneity. Can’t say based on this output

Optional: Pitfalls of Meta-Regression

Skip this section if you are pressed for time.

Multicollinearity

When performing the analysis above, we saw a warning message:

#> Warning: Redundant predictors dropped from the model.

This warning tells us that some of the moderators conveyed exactly the same information, and therefore, it’s not possible to include both in the same model.

For example, look at the following subset of the data. Imagine that this would be our entire dataset:

df[c(5, 24, 28, 46), c("age", "location", "interventioncode", "controlcode", "outcomecode")]
#>      age location   interventioncode      controlcode outcomecode
#> 5  21.00   Canada Prosocial Spending        Self Help       Other
#> 24 20.00   Canada Prosocial Spending        Self Help   Happiness
#> 28 18.55      USA   Acts of Kindness Neutral Activity       Other
#> 46 29.95      USA   Acts of Kindness Neutral Activity       Other

Note that the variable age has unique values for each study, but the first two and second two studies are completely identical in the variables location, interventioncode, and controlcode. If this was our dataset, it would thus not be possible to determine a unique effect for any of these three variables (because they overlap completely). This is an example of (multi)colinearity. Even more worrying: the column outcomecode almost has the same value for each study. If it did, then this column would be redundant with the model’s intercept! It would no longer be a variable, but a constant. As it stands, only one study is distinct in outcomecode. If we add a dummy for this variable - that dummy uniquely identifies that one study (which means the model will perfectly reproduce its value)!

Overfitting

To better understand the risks of (multiple) meta-regression models, we have to understand the concept of overfitting. Overfitting occurs when we build a statistical model which fits the data too closely. In essence, this means that we build a statistical model which can predict the data at hand very well, but performs bad at predicting future data it has never seen before. This happens if our model assumes that some variation in our data stems from a true “signal” in our data, when in fact we only model random noise (Hastie, Tibshirani, and Friedman 2009). As a result, our statistical model produces false positive results: it sees relationships where there are none.

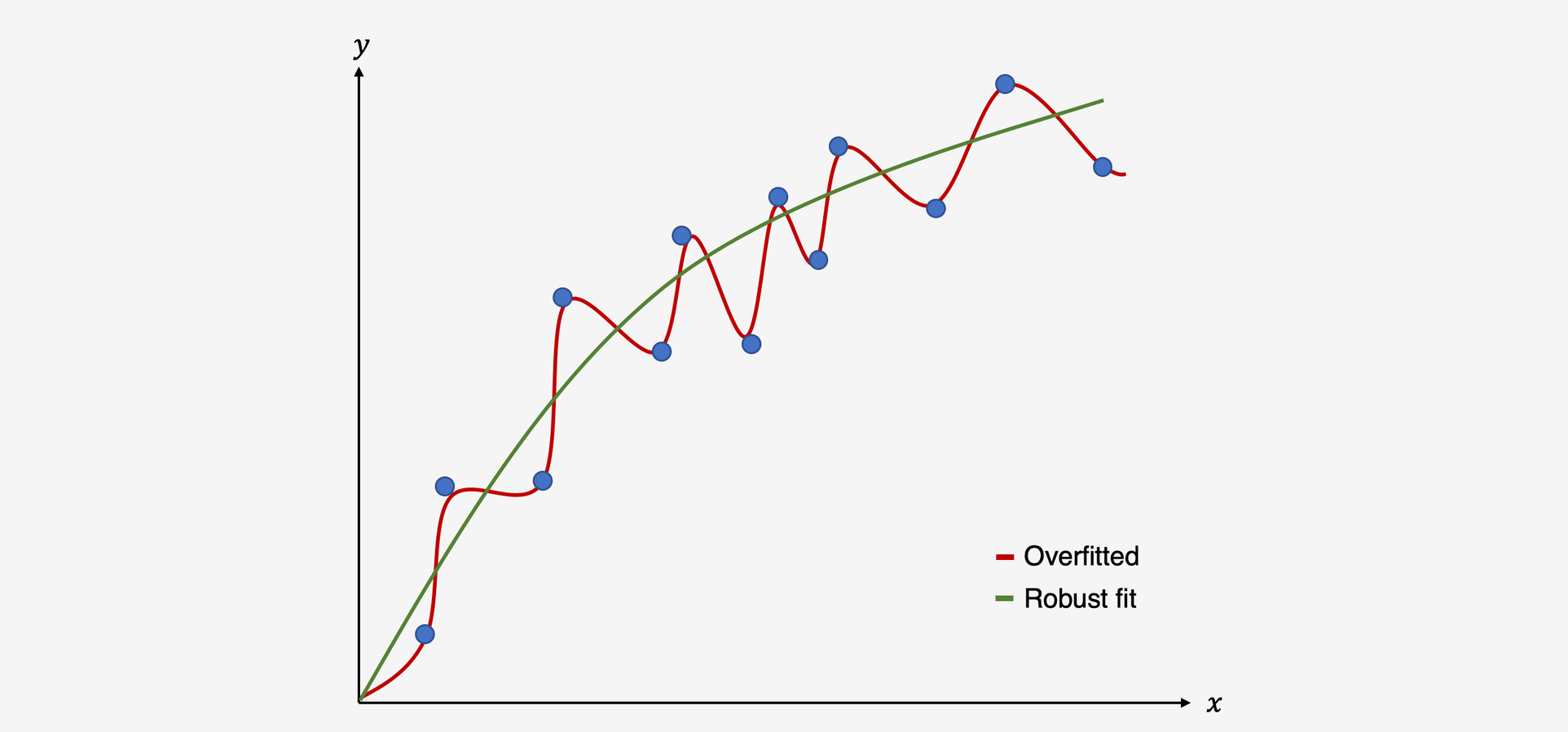
Illustration of an overfitted model vs. model with a good fit

Regression methods, which usually utilize minimization or maximization procedures such as Ordinary Least Squares or Maximum Likelihood estimation, can be prone to overfitting (Hastie, Tibshirani, and Friedman 2009). Unfortunately, the risk of building a non-robust model, which produces false-positive results, is even higher once we go from conventional regression to meta-regression (J. P. T. Higgins and Thompson 2004). There are several reasons for this:

1. In Meta-Regression, our sample is often small, as we can only use the synthesized data of all analyzed studies $k$.
2. As our meta-analysis aims to be a comprehensive overview of all evidence, we have no additional data on which we can “test” how well our regression model can predict high or low effect sizes.
3. In meta-regressions, we have to deal with the potential presence of effect size heterogeneity. Imagine a case in which we have two studies with different effect sizes and non-overlapping confidence intervals. Every variable which has different values for the different studies might be a potential explanation for effect size difference we find, while it seems straightforward that most of such explanations are spurious (J. P. T. Higgins and Thompson 2004).
4. Meta-regression as such, and multiple meta-regression in particular, make it very easy to “play around” with predictors. We can test numerous meta-regression models, include many more predictors or remove them in an attempt to explain the heterogeneity in our data. Such an approach is of course tempting, and often found in practice, because we, as meta-analysts, want to find a significant model which explains why effect sizes differ (J. Higgins et al. 2002). However, such behavior massively increases the risk of spurious findings (J. P. T. Higgins and Thompson 2004), because we can change parts of our model indefinitely until we find a significant model, which is then very likely to be overfitted (i.e., it mostly models statistical noise).

Some guidelines have been proposed to avoid an excessive false positive rate when building meta-regression models:

• Minimize the number of investigated predictors a priori. Predictor selection should be based on predefined scientific or theoretical questions we want to answer in our meta-regression.
• When evaluating the fit of a meta-regression model, we prefer models which achieve a good fit with less predictors. Use fit indices that balance fit and parsimony, such as the Akaike and Bayesian information criterion, to determine which model to retain if you compare several models.
• When the number of studies is low (which is very likely to be the case), and we want to compute the significance of a predictor, you can use the Knapp-Hartung adjustment to obtain more reliable estimates (J. Higgins et al. 2002), by specifying test = "knha when calling rma().

Penalized Meta-Regression

Meta-regression can be used to account for potentially relevant between-studies differences. However, we previously saw that the number of candidate moderators is often high relative to the number of studies. This introduces risks of overfitting, spurious results, and model non-convergence. Bayesian Regularized Meta-Analysis (BRMA) overcomes these challenges, selecting relevant moderators by shrinking small regression coefficients towards zero with regularizing (LASSO or horseshoe) priors (Van Lissa, van Erp, and Clapper 2023). This method is suitable when there are many potential moderators, but it is not known beforehand which of them are relevant.

Let’s use Bayesian regularized meta-regression (BRMA) to select relevant moderators!

First, load in the necessary packages. If you are running the model locally on a multi-core machine, you can set options(mc.cores = 4). This runs 4 MCMC chains in parallel, giving you multiple independent sampling chains while keeping estimation time relatively short.

library(pema)
library(tidySEM)
library(ggplot2)
options(mc.cores = 4)

Two-level model

First, for simplicity, we run a two-level BRMA model, ignoring the fact that certain effect sizes come from the same study.

df_brma <- df[, c("yi", "vi", mods)]

Two-level model with the lasso prior

We start with running a penalized meta-analysis using the lasso prior. Compared to the horseshoe prior, the lasso is easier to use because it has only two hyperparameters to set. However, the lighter tails of the lasso can result in large coefficients being shrunken too much towards zero thereby leading to potentially more bias compared to the regularized horseshoe prior.

For the lasso prior, we need to specify the degrees of freedom df and the scale. Both default to 1. The degrees of freedom determines the chi-square prior that is specified for the inverse-tuning parameter. Increasing the degrees of freedom will allow larger values for the inverse-tuning parameter, leading to less shrinkage. Increasing the scale parameter will also result in less shrinkage. The influence of these hyperparameters can be visualized through the implemented shiny app, which can be called via shiny_prior(), and by calling plot(sample_prior()).

set.seed(1)
fit_lasso <- brma(yi ~ .,
                  data = df_brma,
                  vi = "vi",
                  method = "lasso",
                  prior = c(df = 1, scale = 1),
                  mute_stan = FALSE)

Assessing convergence and interpreting the results

We can request the results using the summary function. Before we interpret the results, we need to ensure that the MCMC chains have converged to the posterior distribution. Two helpful diagnostics provided in the summary are the number of effective posterior samples n_eff and the potential scale reduction factor Rhat. n_eff is an estimate of the number of independent samples from the posterior. Ideally, the ratio n_eff to total samples is as close to 1 as possible. Rhat compares the between- and within-chain estimates and is ideally close to 1 (indicating the chains have mixed well). Should any values for n_eff or Rhat be far from these ideal values, you can try increasing the number of iterations through the iter argument. By default, the brma function runs four MCMC chains with 2000 iterations each, half of which is discarded as burn-in. As a result, a total of 4000 iterations is available on which posterior summaries are based. If this does not help, non-convergence might indicate a problem with the model specification.

sum <- summary(fit_lasso)
sum$coefficients[, c("mean", "sd", "2.5%", "97.5%", "n_eff", "Rhat")]

	mean	sd	2.5%	97.5%	n_eff	Rhat	Sig
Intercept	-20.73	14.41	-50.96	3.62	1656.95	1
mTimeLength	0.00	0.00	-0.01	0.00	2070.44	1
year	0.01	0.01	0.00	0.03	1659.60	1
modelLG	0.09	0.14	-0.18	0.40	2283.22	1
modelLNB	0.14	0.11	-0.03	0.37	1209.83	1
modelM	0.02	0.05	-0.07	0.13	2208.18	1
modelMD	0.02	0.08	-0.13	0.19	2319.51	1
ageWeek	-0.01	0.01	-0.02	0.00	1363.64	1
strainGroupedC57Bl6	-0.02	0.07	-0.16	0.11	2192.98	1
strainGroupedCD1	-0.12	0.18	-0.53	0.20	2073.86	1
strainGroupedDBA	-0.03	0.16	-0.36	0.31	1591.17	1
strainGroupedlisterHooded	-0.05	0.31	-0.71	0.54	2062.04	1
strainGroupedlongEvans	0.07	0.12	-0.14	0.34	2253.15	1
strainGroupedlongEvansHooded	0.18	0.22	-0.18	0.66	2301.79	1
strainGroupedNMRI	0.12	0.24	-0.33	0.65	2224.83	1
strainGroupedNS	0.03	0.15	-0.27	0.34	2842.07	1
strainGroupedother	-0.02	0.13	-0.28	0.23	2079.33	1
strainGroupedspragueDawley	0.00	0.06	-0.13	0.12	1921.19	1
strainGroupedswissWebster	0.56	0.49	-0.23	1.64	2230.04	1
strainGroupedwistar	0.02	0.06	-0.08	0.15	2078.13	1
strainGroupedwistarKyoto	0.03	0.27	-0.53	0.58	2391.66	1
bias	-0.01	0.03	-0.07	0.05	2087.24	1
speciesrat	0.12	0.09	-0.02	0.32	1379.54	1
domainsLearning	0.00	0.05	-0.10	0.11	1985.97	1
domainnsLearning	0.12	0.08	-0.02	0.29	1552.84	1
domainsocial	0.17	0.12	-0.02	0.42	1599.73	1
domainnoMeta	-0.36	0.18	-0.73	-0.02	1212.41	1	*
sexM	0.12	0.07	0.00	0.26	1602.07	1
tau2	0.43	0.04	0.35	0.51	1112.00	1	*

If we are satisfied with the convergence, we can continue looking at the posterior summary statistics. The summary function provides the posterior mean estimate for the effect of each moderator. Since Bayesian penalization does not automatically shrink estimates exactly to zero, some additional criterion is needed to determine which moderators should be selected in the model. Currently, this is done using the 95% credible intervals, with a moderator being selected if zero is excluded in this interval. In the summary this is denoted by an asterisk for that moderator.

Also note the summary statistics for tau2, the (unexplained) residual between-studies heterogeneity.

Formative Assessment

How many significant moderator effects are there? TRUE FALSE

True or false: There is significant residual heterogeneity. TRUE FALSE

What can we say about the coefficients of this BRMA analysis, compared to the previous rma() multiple regression? All absolute BRMA coefficients are smaller than RMA coefficients. The BRMA coefficients are more variable than RMA coefficients. It is easier for coefficients to be significant in BRMA than in RMA. The answer depends on the specific analysis.

Optional: Three-level model with Horseshoe Prior

The default prior in brma() is the horseshoe prior, because it performed best in simulation studies. Moreover, we can take into account the fact that some effect sizes might come from the same study by fitting a three-level model as follows:

df_brma_threelevel <- df[, c("yi", "vi", "study_id", mods)]
set.seed(7)
fit_hs <- brma(yi ~ .,
               data = df_brma_threelevel,
               vi = "vi",
               study = "study_id")

More Information

Reference: Van Lissa, van Erp, and Clapper (2023)

For a more elaborate tutorial, see this vignette.

Random Forest Meta-Regression

BRMA is comparable to multiple meta-regression, with the main difference being that it shrinks coefficients towards zero to eliminate irrelevant moderators. An alternative machine learning-informed approach to moderator selection is to use tree-based methods. In this section, we use MetaForest - a random forest-based approach - to analyze the same data and select relevant moderators (Van Lissa 2020).

# Load the metaforest package
library(metaforest)
#> Loading required package: metafor
#> Loading required package: Matrix
#> Loading required package: metadat
#> Loading required package: numDeriv
#> 
#> Loading the 'metafor' package (version 4.8-0). For an
#> introduction to the package please type: help(metafor)
#> Loading required package: ranger
#> Loading required package: data.table

Check Convergence

For any random forest model, it is important to determine how many trees are needed to get stable results. Convergence is indicated by stabilization of the cumulative mean squared out-of-bag prediction error (MSEoob), as a function of the number of trees in the model. We run the analysis once with a very high number of trees, and pick a smaller number of trees, at which the model is also seen to have converged, to speed up computationally heavy steps, such as replication and model tuning. We re-examine convergence for the final model. Note that we can account for multiple effect sizes per study in MetaForest as well:

# Run model with many trees to check convergence
set.seed(74)
check_conv <- MetaForest(yi~.,
data = df_brma_threelevel,
study = "study_id",
whichweights = "random",
num.trees = 10000)
# Plot convergence trajectory
plot(check_conv)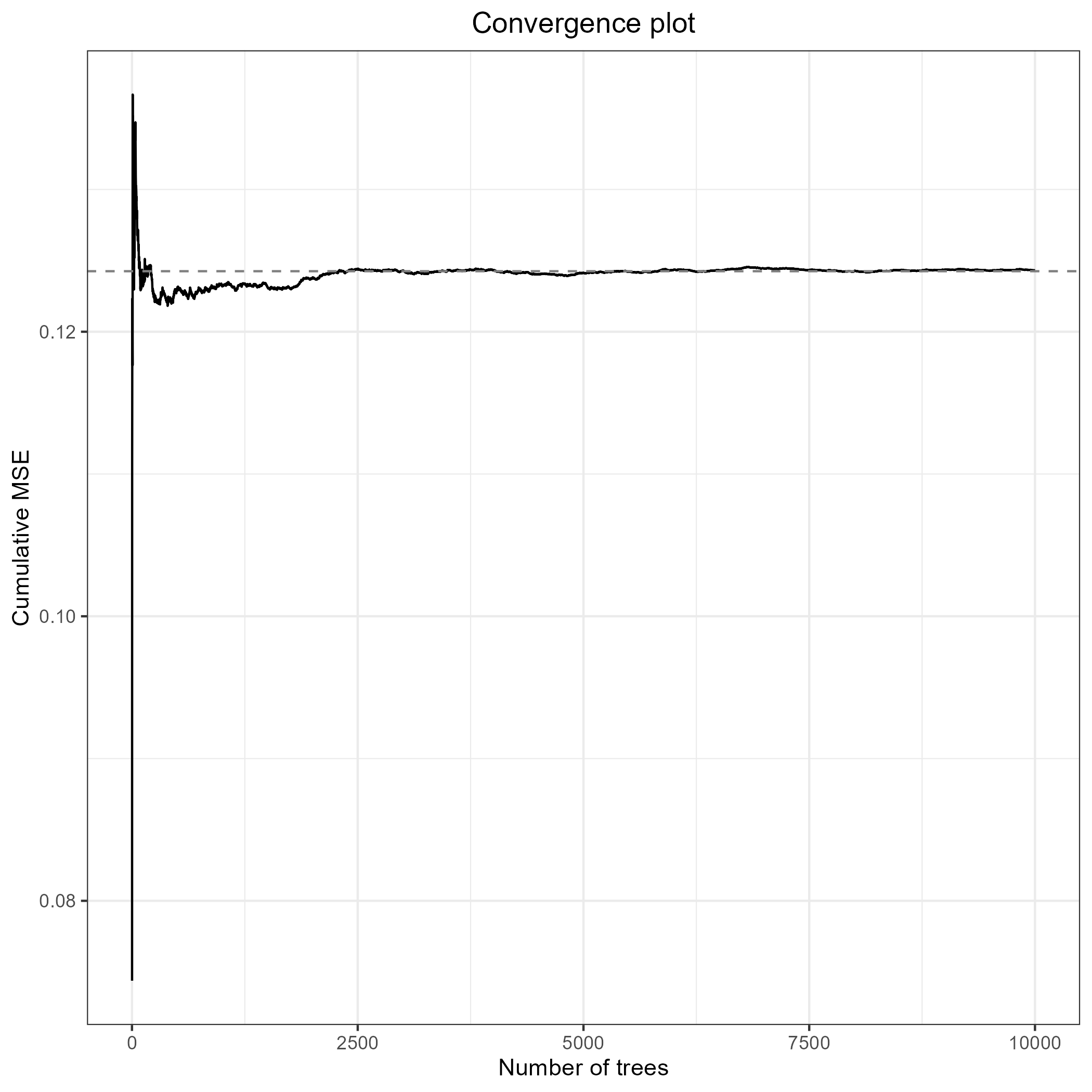

This model converges at around 2500 trees.

Model Tuning

Machine learning models often have hyperparameters that must be tuned to get good performance for a specific learning task. We can tune the model using the R package caret. As tuning parameters, we consider all three types of weights (uniform, fixed-, and random-effects), the number of candidate variables at each split from 2–6, and a minimum node size from 2–6. We select the model with smallest root mean squared prediction error (RMSE) as the final model, based on 5-fold clustered cross-validation. Clustered cross-validation means that effect sizes from the same study are always included in the same fold, to account for the dependency in the data. Note that the number of folds cannot exceed the number of clusters in the data. Moreover, if the number of clusters is very small, one might have to resort to specifying the same number of folds as clusters. Model tuning is computationally intensive and might take a long time.

# Load caret
library(caret)
# Set up 5-fold clustered CV
grouped_cv <- trainControl(method = "cv",
index = groupKFold(df_brma_threelevel$study_id, k = 5))

# Set up a tuning grid
tuning_grid <- expand.grid(whichweights = c("random", "fixed", "unif"),
mtry = 2:6,
min.node.size = 2:6)
# X should contain only retained moderators, clustering variable, and vi
X <- df_brma_threelevel[, c("study_id", "vi", mods)]
# Train the model
set.seed(3)
mf_cv <- train(y = df_brma_threelevel$yi,
x = X,
study = "study_id", # Name of the clustering variable
method = ModelInfo_mf(),
trControl = grouped_cv,
tuneGrid = tuning_grid,
num.trees = 2500)
# Best model tuning parameters
mf_cv$results[which.min(mf_cv$results$RMSE), ]

#>    whichweights mtry min.node.size      RMSE  Rsquared       MAE     RMSESD
#> 32        fixed    3             3 0.2760904 0.2936028 0.2240218 0.08613236
#>    RsquaredSD      MAESD
#> 32  0.2951682 0.06719638

Based on the root mean squared error, the best combination of tuning parameters were fixed-effect weights, with three candidate variables per split, and a minimum of three cases per terminal node.

Interpreting the Results

The object returned by train already contains the final model, estimated with the best combination of tuning parameters.

# Extract final model
final <- mf_cv$finalModel
# Extract R^2_oob from the final model
r2_oob <- final$forest$r.squared

This model has a positive estimate of explained variance in new data, $R^2_{oob} = .19$.

Now, we proceed to interpreting the moderator effects, by examining variable importance and partial dependence plots. Variable importance is determined by randomly permuting each variable in turn (so it loses all meaningful association with the outcome), and then assessing how much the model’s predictive performance diminishes after this random permutation. For an important variable, the model performance drops after permutation. Partial dependence plots show the model’s predicted values at different levels of one variable, averaging over the values of all other variables. Thus, you can think of this as the bivariate marginal association.

# Plot variable importance
VarImpPlot(final)

# Sort the variable names by importance
ordered_vars <- names(final$forest$variable.importance)[
order(final$forest$variable.importance, decreasing = TRUE)]

# Plot partial dependence
PartialDependence(final, vars = ordered_vars,
rawdata = TRUE, pi = .95)

Formative Assessment

What does the negative permutation importance for donorcode indicate? Prosocial Spending Other Acts of Kindness

Which intervention has the lowest associated effect size? Randomly permuting this variable improves model fit This variable has a positive effect on the outcome (effect size) Randomly permuting this variable diminishes model fit This variable has a negative effect on the outcome (effect size)

Which variable has apparent outlier(s)? donorcode outcomecode age

More Information

Reference: Van Lissa (2020)

For a more elaborate tutorial, see this open access book chapter on MetaForest.

Bayesian Evidence Synthesis

Heterogeneity presents a fundamental challenge to research synthesis methods (J. P. T. Higgins, Thompson, and Spiegelhalter 2009). When studies all assess the same informative hypothesis, but differ in fundamental ways that preclude aggregation through conventional meta-analysis methods, Bayesian Evidence Synthesis (BES) can be used. Consider, for example, the situation that arises when the number of moderators is very large relative to the number of studies, or when moderators are redundant (see Meta-Regression chapter above).

The PBF (Van Lissa, Kuiper, and Clapper 2023) can be used instead of random-effects meta-analysis when its assumptions were likely to be violated. This Tutorial illustrates the use of the PBF in such cases.

At the start of the day, we conducted random- and fixed effects meta-analyses using the function rma() from the metafor package. This required the yi and vi columns. Now, we will perform a PBF analysis using the pbf() function in the bain package, which accepts the same arguments.

First, we will load the required packages.

library(bain)

Repeating the RMA

Let’s repeat our previous random effects meta-analysis, and examine a funnel plot of the distribution of effect sizes:

res_rma <- rma(yi = yi, vi = vi, data = df)
funnel(res_rma)

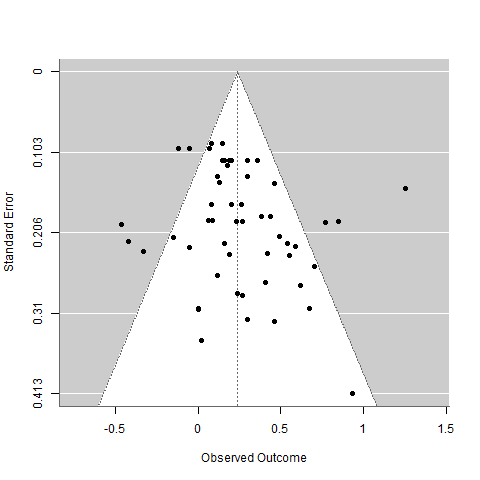
An effect size over 0 means that helping others increased happiness, even a little bit.

With a Bayes Factor, we could test the informative hypothesis (just a directional null hypothesis) that helping increases happiness in one particular study, for example the first row of the dataset:

set.seed(1)
bain(x = c("yi" = df$yi[1]), # Select the first effect size
     Sigma = matrix(df$vi[1], 1, 1), # Make covariance matrix
     hypothesis = "yi > 0", # Define informative hypothesis
     n = df$n1i[1]+df$n2c[1]) # Calculate total sample size
#> Bayesian informative hypothesis testing for an object of class numeric:
#> 
#>    Fit   Com   BF.u  BF.c     PMPa  PMPb  PMPc 
#> H1 0.999 0.500 1.999 1508.434 1.000 0.667 0.999
#> Hu                                  0.333      
#> Hc 0.001 0.500 0.001                      0.001
#> 
#> Hypotheses:
#>   H1: yi>0
#> 
#> Note: BF.u denotes the Bayes factor of the hypothesis at hand versus the unconstrained hypothesis Hu. BF.c denotes the Bayes factor of the hypothesis at hand versus its complement. PMPa contains the posterior model probabilities of the hypotheses specified. PMPb adds Hu, the unconstrained hypothesis. PMPc adds Hc, the complement of the union of the hypotheses specified.

The results indicate that the first study provides 1508 times more evidence in favor of our informative hypothesis (helping increases happiness) than against it, $BF = 1508.434$.

Product Bayes Factor

We now perform the PBF analysis, using the pbf() method for numeric input (see ?pbf). This interface is very similar to rma(), and is specifically designed for applications where PBF is applied to meta-analytic datasets. The yi and vi arguments are the same as those of rma(). Additional argument ni is used to construct the prior for the approximate Bayes factors (Hoijtink et al. 2019). Importantly, the hypothesis argument determines which informative hypotheses are tested.

set.seed(1)
res_pbf <- pbf(yi = df$yi,
               vi = df$vi,
               ni = sum(df$n1i+df$n2c),
               hypothesis = "y > 0")

	PBF	Sample.1	Sample.2	Sample.3
H1: y>0	7.449242e+69	1508.434	4.579145	81.31709

The resulting output shows the product Bayes factors for our informative hypothesis (PBF column), as well as study-specific Bayes factors (remaining columns, trimmed here to keep the document tidy). The PBF in favor of our hypothesis is very high (a 7.45 with 69 zeroes), so the body of evidence provides consistent support for the notion that helping increases happiness.

Formative Assessment

What does a negative Bayes factor indicate, for a Bayes factor comparing an informative hypothesis Hi against its complement Hc? Negative Bayes factors don’t exist The evidence for Hc outweighs the evidence for Hi The evidence for Hi outweighs the evidence for Hc The evidence for Hi outweighs the evidence for Hc, but the effect is negative

True or false: All Bayes factors must exceed one (BF > 1) to obtain a PBF that also exceeds one (PBF > 1) TRUE FALSE

True or false: A large Bayes factor means that the hypothesized effect likely exists in the population TRUE FALSE

This last question relates to generalizability. When we perform a normal fixed- or random-effects meta-analysis, we rely on sampling theory and assume that each effect size represents a random sample from the population of possible effect sizes.

If this assumption is justified, then we can claim that the pooled effect size generalized to the population those effect sizes were randomly sampled from. Thus, our pooled effect size tells us something about future studies.

Of course, this assumption is very questionable, due to publication bias, and the fact that researchers build upon previous work! So in practice, meta-analysis might not be as generalizable as we’d like.

The PBF does not rely on sampling theory and does not make such assumptions about random sampling from the population. As a result, it can only be interpreted as a quantitative summary of the evidence within the present sample of studies.

It would be incorrect to interpret the PBF as saying anything about the population; we should interpret it as a summary statistic of the studies at hand. Of course, the same could be said about conventional meta-analysis, if the assumption of random sampling is violated.

More Information

References: Van Lissa, Kuiper, and Clapper (2023), Van Lissa et al. (2020)

For a more elaborate tutorial on the Product Bayes Factor, see this paper, in press at Research Synthesis Methods.

Credit

This tutorial is partly based on the book Doing Meta-Analysis with R: A Hands-On Guide, which is also recommended as further reading:

Harrer, M., Cuijpers, P., Furukawa, T.A., & Ebert, D.D. (2021). Doing Meta-Analysis with R: A Hands-On Guide. Boca Raton, FL and London: Chapmann & Hall/CRC Press. ISBN 978-0-367-61007-4.

References

Borenstein, Michael, Larry V. Hedges, Julian P. T. Higgins, and Hannah R. Rothstein. 2009. Introduction to Meta-Analysis. John Wiley & Sons, Ltd. https://doi.org/10.1002/9780470743386.

Hastie, Trevor, Robert Tibshirani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second. New York: Springer.

Higgins, Julian P. T., and Simon G. Thompson. 2004. “Controlling the Risk of Spurious Findings from Meta-Regression.” Statistics in Medicine 23 (11): 1663–82. https://doi.org/10.1002/sim.1752.

Higgins, Julian P. T., Simon G. Thompson, and David J Spiegelhalter. 2009. “A Re-Evaluation of Random-Effects Meta-Analysis.” Journal of the Royal Statistical Society. Series A, (Statistics in Society) 172 (1): 137–59. https://doi.org/10.1111/j.1467-985X.2008.00552.x.

Higgins, Julian, Simon Thompson, Jonathan Deeks, and Douglas Altman. 2002. “Statistical Heterogeneity in Systematic Reviews of Clinical Trials: A Critical Appraisal of Guidelines and Practice.” Journal of Health Services Research & Policy 7 (1): 51–61. https://doi.org/10.1258/1355819021927674.

Hoijtink, Herbert, Joris Mulder, Caspar van Lissa, and Xin Gu. 2019. “A Tutorial on Testing Hypotheses Using the Bayes Factor.” Psychological Methods 24 (5): 539–56. https://doi.org/10.1037/met0000201.

Schwarzer, Guido, James R. Carpenter, and Gerta Rücker. 2015. Meta-Analysis with R. Use R! Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-21416-0.

Van Lissa, Caspar J. 2020. “Small Sample Meta-Analyses: Exploring Heterogeneity Using MetaForest.” In Small Sample Size Solutions (Open Access): A Guide for Applied Researchers and Practitioners, edited by Rens Van De Schoot and Milica Miočević. European Association of Methodology Series. CRC Press.

Van Lissa, Caspar J., Sara van Erp, and Eli-Boaz Clapper. 2023. “Selecting Relevant Moderators with Bayesian Regularized Meta-Regression.” Research Synthesis Methods 14 (2): 301–22. https://doi.org/10.1002/jrsm.1628.

Van Lissa, Caspar J., Xin Gu, Joris Mulder, Yves Rosseel, Camiel Van Zundert, and Herbert Hoijtink. 2020. “Teacher’s Corner: Evaluating Informative Hypotheses Using the Bayes Factor in Structural Equation Models.” Structural Equation Modeling: A Multidisciplinary Journal 0 (0): 1–10. https://doi.org/10.1080/10705511.2020.1745644.

Van Lissa, Caspar J., Rebecca M. Kuiper, and Eli-Boaz Clapper. 2023. “Aggregating Evidence from Conceptual Replication Studies Using the Product Bayes Factor.” Preprint. PsyArXiv. https://doi.org/10.31234/osf.io/nvqpw.

Viechtbauer, Wolfgang. 2010. “Conducting Meta-Analyses in R with the Metafor Package.” Journal of Statistical Software 36 (3): 1–48.